Moving Iron Type Instruments

The general principle of working of a moving iron instrument (which is strictly relevant to attraction type of moving iron instruments) can be explained as under:

A plate or vane of soft iron or of high permeability steel forms the moving element of the system. This iron vane is so situated that it can move in a magnetic field produced by a stationary coil. The coil is excited by the current or voltage under measurement. When the coil is excited, it becomes an electromagnet and the iron vane moves in such a way so as to increase the flux of the electromagnet. This is because the vane tries to occupy a position of minimum reluctance. Thus, the force produced is always in such direction so as to increase the inductance of coil (this is because inductance is inversely proportional to reluctance of magnetic circuit of the coil).

An expression for the torque of a moving iron instrument may be derived by considering the energy relations when there is a small increment in current supplied to the instrument. When this happens there will be a small deflection dθ and some mechanical work will be done. Let T_d be the deflecting torque.

Mechanical work done = T_d dθ

Alongside there will be a change in the energy stored in the magnetic field owing to change in inductance. Suppose the initial current is I, the instrument inductance L and the deflection θ. If the current increases by dI then the deflection changes by dθ and the inductance by dL. In order to affect an increment dI in the current there must be an increase in the applied voltage given by

$$e=\frac{d}{dt}\left( LI \right)=I\frac{dL}{dt}+L\frac{dI}{dt}$$

The electrical energy supplied, $$eIdt={{I}^{2}}dL+ILdI$$

The stored energy changes from \[\frac{1}{2}{{I}^{2}}L\] to $$\frac{1}{2}{{\left( I+dI \right)}^{2}}+\left( L+dL \right)$$

Hence the change in stored energy, \[\frac{1}{2}{{\left( I+dI \right)}^{2}}+\left( L+dL \right)-\frac{1}{2}{{I}^{2}}L\]

Neglecting second and higher order terms in small quantities this becomes \[ILdI+\frac{1}{2}{{I}^{2}}dL\]

From the principle of conservation of energy,

Electrical energy supplied = Increase in stored energy + Mechanical work done

\[{{I}^{2}}dL+ILdI=ILdI+\frac{1}{2}{{I}^{2}}dL+{{T}_{d}}\,d\theta \]

Thus, deflecting torque, \[{{T}_{d}}=\frac{1}{2}{{I}^{2}}\frac{dL}{d\theta }\]

T is in newton-metre, I in ampere, L in henry, and θ in radian.

The moving system is provided with control springs and it turns the deflecting torque T_d is balanced by the controlling torque, T_C = Kθ.

where K = control spring constant in Nm/rad,

θ – deflection in radian

At equilibrium (or final steady) position, T_C =T_d

Deflection, \[\theta =\frac{1}{2}\frac{{{I}^{2}}}{K}\frac{dL}{d\theta }\]

Hence the deflection is proportional to square of the rms value of the operating current. The deflecting torque is, therefore, unidirectional (acts in the same direction) whatever may be the polarity of the current.

Moving iron instruments are of two types:

(i) Attraction type.

(ii) Repulsion type.

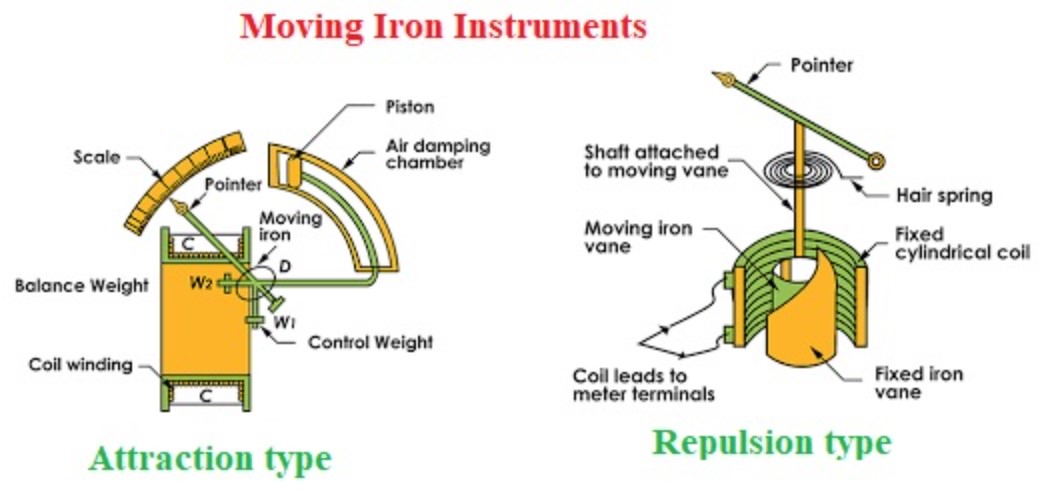
(i) Attraction type

Figure shows the constructional details of an attraction type moving iron instrument. The coil is flat and has a narrow slot like opening. The moving iron is a flat disc or a sector eccentrically mounted. When the current flows through the coil, a magnetic field is produced and the moving iron moves from the weaker field outside the coil to the stronger field inside it or in other words, the moving iron is attracted in. The controlling torque is provided by springs but gravity control can be used for panel type of instruments which are vertically mounted.

Fig: Attraction type moving iron instrument

Damping is provided by air friction with the help of a light aluminium piston (attached to the moving system) which moves in a fixed chamber closed at one end as shown in Figure or with the help of a vane (attached to the moving system) which moves in a fixed sector shaped chamber.

(ii) Repulsion type

In the repulsion type, there are two vanes inside the coil one fixed and other movable. These are similarly magnetised when the current flows through the coil and there is a force of repulsion between the two vanes resulting in the movement of the moving vane. Two different designs are in common use:

(i) Radial Vane Type: In this type, the vanes are radial strips of iron. The strips are placed within the coil as shown in Fig. (a). The fixed vane is attached to the coil and the movable one to the spindle of the instrument.

(ii) Co-axial Vane Type: In this type of instrument, the fixed and moving vanes are sections of co-axial cylinders as shown in Fig. (b). The controlling torque is provided by springs. Gravity control can also be used in vertically mounted instruments. The damping torque is produced by air friction as in attraction type instruments.

Fig: Repulsion type moving iron instrument

The operating magnetic field in moving iron instruments is very weak and therefore eddy current damping is not used in them as introduction of a permanent magnet required for eddy current damping would distort the operating magnetic field.

It is clear that whatever may be the direction of the current in the coil of the instrument, the iron vanes are so magnetised that there is always a force of attraction in the attraction type and repulsion in the repulsion type of instruments. Thus, moving iron instruments are unpolarised instruments i.e., they are independent of the direction in which the current passes. Therefore, these instruments can be used on both ac and dc.

The deflecting torque is proportional to the square of current multiplied by the rate of change of inductance with angle. The scale is compressed at its lower end because I² is small relative to full scale value and somewhat compressed at its higher end because in this range the rate of change of inductance with angle (i.e., dL/dθ) decreases rapidly.

Advantages and Disadvantages of Moving Iron Instruments

• Universal use: These instruments can be used for both ac and dc.
• Less friction errors: Errors due to friction are quite small as torque-weight ratio is quite high.
• Cheapness: A single type of moving element could cover the entire range is one reason that moving iron instruments can be built at less cost than some other types.
• Robustness: The instruments are robust owing to simple construction and also that there are no current carrying moving parts.
• Accuracy: These instruments are capable of giving an accuracy within the limits of both precision and industrial grades.
• Scale: The scale of moving iron instruments is not uniform and is cramped at the lower end.
• Errors: These instruments are subjected to serious errors due to hysteresis, frequency changes and stray magnetic fields.